Introduction

This project uses reinforcement learning to encourage the language model roneneldan/TinyStories-33M to generate stories with alliteration.

Code here

Demo

Here’s a non-cherry-picked generation from the unmodified model:

Once upon a time there was a cute little bunny named Fluff. Fluff was a very clever bunny who liked to explore and find new places every day. One day while Fluff was hopping around, he noticed a big knot in a tree. He wanted to attach the knot to something, so he used his paws to attach it. Fluff hopped up to the nearest rabbit and said, “Hello, can you help me attach this knot to the tree?” The

By coincidence, there are some consecutive words with the same initial letter, such as Fluff. Fluff and to the tree?" The.

Here’s a generation from the model after reinforcement learning:

Once upon a time, there was a tall tree. The tall tree was in the middle of a park. One day, a little girl wanted to touch the tall tree. She started to walk towards the tall tree. When she got to the tall tree, she started to touch the branches. Suddenly, the tree started to grow taller and taller! The little girl was amazed and she ran away from the tall tree. She kept running and she forgot about the tall tree. She

(Here I chose the first generation after step 5000.)

Now there’s much more alliteration, such as to touch the tall tree, She started, and towards the tall tree.

Note on definitions

For simplicity, I’m defining alliteration as two or more consecutive words with the same initial letter. So “Zebadiah the Zebra” doesn’t count because of the intermediate “the”, and “seven cycling psychologists” doesn’t count even though the initial sound is the same.

The exact reward function is

def get_raw_reward(text: str) -> int:
    words = text.split()
    return sum(
        1
        for word, next_word in zip(words, words[1:])
        if word[0].lower() == next_word[0].lower()
    )

REINFORCE vs RLOO

How is reinforcement learning different from supervised learning?

In supervised learning, we want to train the model to accurately predict labels given inputs. For instance, the input might be “the position of all the pieces on a chess board”, and the label might be “which side has the advantage, as estimated by a human judge”. The dataset looks like a list of (input, label) tuples.

In reinforcement learning, we instead want to train the model to produce good actions, as measured by some reward function. The action might be “go play a chess game”, and the reward would be “did you win?” Typically there isn’t a fixed dataset of (action, reward) tuples, since the model is taking the actions on the fly.

In my case, the action is “write a story with 100 tokens”, and the reward is “how many words started with A or a?”

The REINFORCE algorithm

If the model produces a story with a high reward, we want to nudge the model to generate stories more like that one.

Procedure:

1. Feed the generated text to the model to get a probability, i.e. how likely the model thinks the text is
2. Use backpropagation to get the gradient of that probability with respect to the model weights.
3. If we add gradient to the weights, we’ll make the model more likely to generate this text sequence, and in theory also more likely to generate similar text sequences.
4. We want to nudge the model more if the reward was higher (and vice versa), so instead we add reward * gradient to the weights.

This is the REINFORCE algorithm. (The REINFORCE paper has variants on this algorithm, so I’m simplifying.)

Let’s apply the REINFORCE algorithm on two identical trains (except for seed):

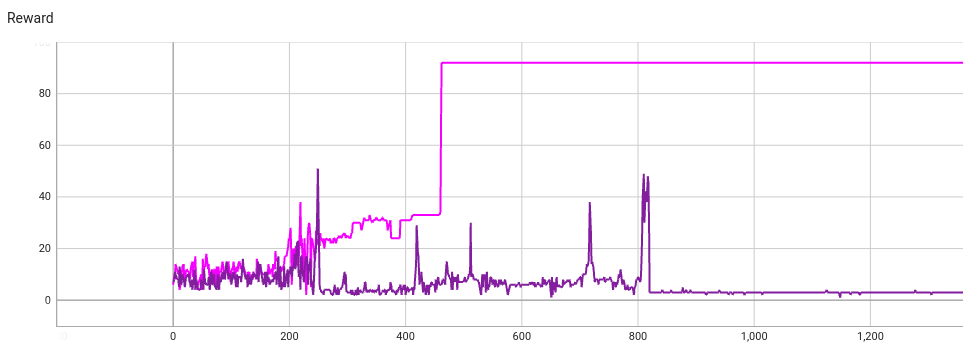
One of the models (pink) finds a high reward text. After step 462 the model predicts that text at every step:

Once upon a time in a big nation with a little a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a

The other train fixates on a different story, except this one has much lower reward:

Once upon a time, a big and the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the

What went wrong with the second train?

The RLOO algorithm

The problem is that the model gets stuck in a local optimum. If the model happens to generate the same text sequence multiple times, then REINFORCE will keep making that text sequence more likely, so the model will keep generating it. Hence the model will inevitably fixate on one particular text. And this text doesn’t have to be a high reward text, as seen above.

The solution is to normalize the reward, using recent rewards as a baseline. If the model generates a text sequence whose reward is higher than those of recent generations, that text sequence should get positive reward after normalization. We want the model to move in this direction.

Conversely, if a text sequence has a reward that’s lower than recent generations’ rewards, the normalized reward should be negative, even if the raw reward is still high. We want to decrease the probability that the model predicts worse-than-normal sequences.

This technique is known as REINFORCE-Leave-One-Out (RLOO—see Ahmadian et al. for more).

Here’s a plot of the reward over time of two RLOO runs (both green), versus the REINFORCE runs above:

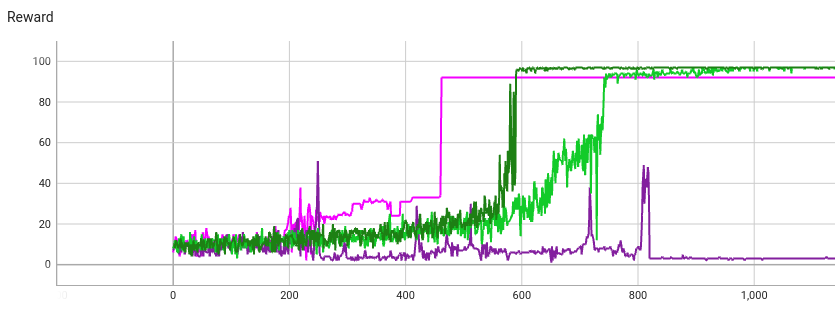
RLOO can take longer to find a high reward, since it has to generate multiple texts (in my case 10) to get an estimate of recent rewards. Hence it only takes 1 optimizer step per 10 generations. The x-axis is the number of text generations (what TensorBoard sees as steps).

But RLOO avoids getting stuck on a low-reward sequence, and its final reward is higher. This is because RLOO is “never satisfied”. If it gets mostly reward 92 but occasionally a reward of 93, RLOO will push the model weights towards reward 93 even though reward 92 is already very good (maximum possible is 97).

Thus the second RLOO run finds this sequence with the highest possible reward:

Once upon a time a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and a and

What is the KL penalty?

Why do we even need the KL penalty?

We could just train a model as-is. If we do, the reward looks great:

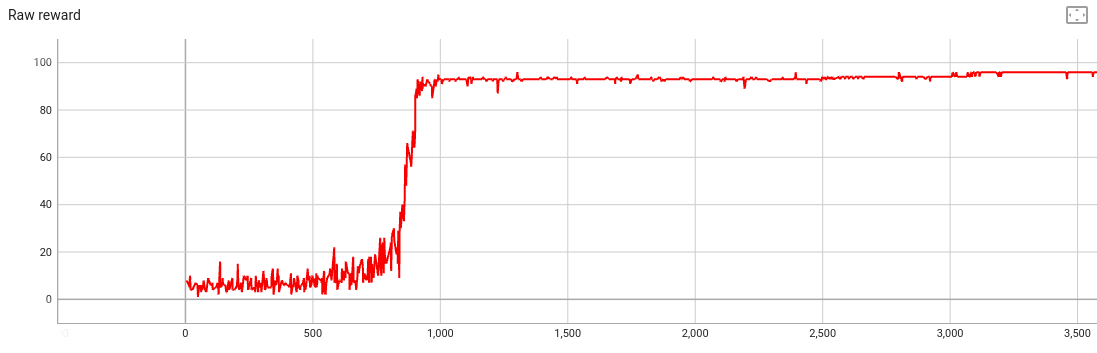
But if we look at the text generations near the end of training, the model always predicts the same 100 words:

Once upon a time to the tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall

Gradient descent has singlemindedly pushed the model weights toward maxmizing the reward function, and we’ve lost important qualities like:

• The model should generate a variety of texts, not the same one every time
• The text should be a story with acceptable grammar and coherence, not just unrelated words

Definition of the KL penalty

KL stands for Kullback–Leibler, as in Kullback–Leibler divergence. The KL divergence can be interpreted as a difference in cross-entropies, and we’ll use that form for the penalty:

kl_penalty_term = beta * (lm_cross_entropy - original_lm_cross_entropy)

where

• beta >= 0 is a hyperparameter controlling the penalty strength
• lm_cross_entropy is the cross entropy loss of the language model on the current text generation
• original_lm_cross_entropy is the cross entropy loss using a copy of the weights before reinforcement learning

We add the kl_penalty_term to raw_reward (i.e. the reward from counting alliteration) and then apply RLOO to that composite reward.

Motivation:

• Suppose that the LM has generated a sequence like “tall tall tall….” This sequence has high raw reward, but since this isn’t coherent English, we’d like the composite reward to be low.
• lm_cross_entropy will be a small positive number, since the LM did generate this text.
• original_lm_cross_entropy will be a large positive number, since the original LM wouldn’t have generated this text.
• Hence the kl_penalty_term will be negative, which will reduce the composite reward.

Tuning the KL penalty

First sweep

We still don’t know what the KL penalty coefficient beta should be. Let’s sweep over the following values:

• beta=0 (red)
• beta=0.01 (orange)
• beta=0.1 (yellow)
• beta=1 (green)
• beta=10 (blue)
• beta=100 (violet)

The raw reward:

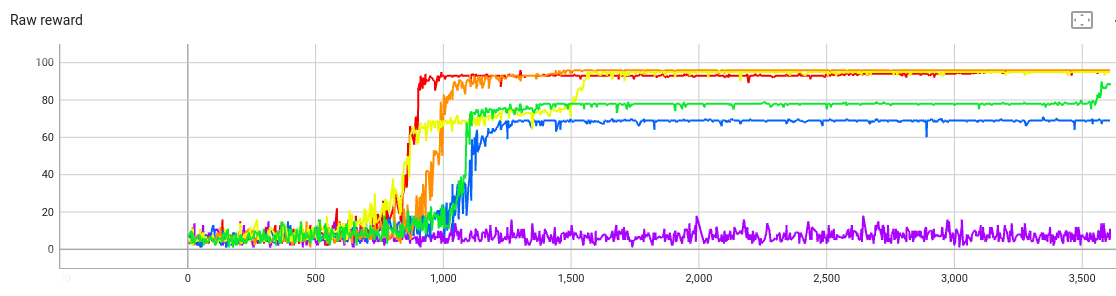
The curves are in roughly the right order: A higher beta shrinks the raw reward.

The KL penalty (before multiplying by beta):

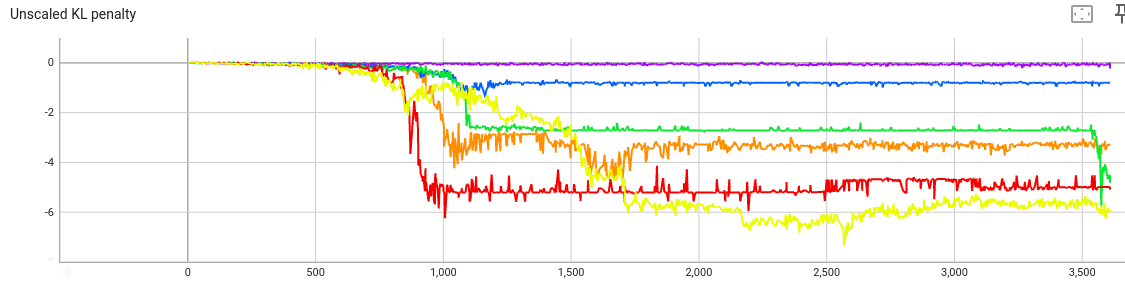
Again, this makes sense: When the penalty coefficient beta is small, gradient descent doesn’t optimize for the KL penalty.

Let’s look at the last two text generations¹ for each train:

• beta=0
  • Last: “Once upon a time to the tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall tall”
  • Second-to-last: The same, except missing “the”
• beta=0.01
  • Last: “Once upon a time to to the tree to the tree to the tree to the tree to the tree to the tree to the tree to the tree to the tree to the tree to the tree to the tree to the tree to to the tree to the tree to the tree to the tree to the tree to the tree to the tree to the tree to to the tree to the tree to the tree to the tree to the tree to the tree to the tree to to the tree to the tree to the”
  • Second-to-last: The same, except with one more “to”
• beta=0.1
  • Last: “Once upon a time there saw something she saw she suddenly suddenly she saw she she suddenly saw suddenly she she she saw she suddenly she she suddenly she she suddenly she saw she she suddenly she saw suddenly she she suddenly suddenly she saw suddenly she suddenly saw she suddenly she saw suddenly she she suddenly she suddenly she saw suddenly she suddenly she she suddenly saw she suddenly she suddenly she she she saw suddenly she she suddenly she suddenly suddenly she saw suddenly she suddenly she she saw suddenly she suddenly saw she suddenly she saw suddenly”
  • Second-to-last: The same, except with one more “she”
• beta=1
  • Last: “Once upon a time there was something special something special something special something special something special something special something special something special. Suddenly she saw something special something special something special something special something special. Suddenly she saw something special something special something special something special she saw something special something special something special. Suddenly she saw something special something special something special something special something special something special she saw something special. Suddenly she saw something special something special something special something special she saw something special something special she saw special something special.”
  • Second-to-last: The same, except the sentences aren’t exactly the same lengths
• beta=10
  • Last: “Once upon a time there was a girl. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something. She saw something”
  • Second-to-last: The same
• beta=100
  • Last: “Once upon a time, there was a little girl. She was very independent and loved to help her mom. One day, she noticed that there was something scary backstage in the library. The little girl was frightened by the display at the building, so she asked her mom to stay close and make sure she was safe. Her mother was teaching her how to stay calm and how to make the noise strongly, so that the images in the theater were not scary.”
  • Second-to-last: “Once upon a time, there was a little girl who liked to play in the rain. Her parents told her that it wasn’t safe, but the little girl couldn’t help but be curious. One day, the girl’s parents said they had a surprise for her. When they revealed it was a brand new toy. The girl couldn’t believe her ears. She quickly hugged her parents and thanked them for the surprise. From then on, the little girl never stopped playing in the”

Conclusions: As beta increases, the text generations become more grammatically correct. From beta=10 to beta=100, the generated text has a step change: The model is no longer writing the same few words over and over. But also at beta=100, the model isn’t very good at alliteration.

You can see this in the reward curve as well. The violet curve (beta=100) has a much lower raw reward, and also its reward varies from step to step, since it’s not always generating the same text.

We’d like varied text and alliteration. Hence the optimal value of beta is somewhere between 10 and 100.

Second sweep

We’ll sweep over these values:

• beta=20 (red)
• beta=30 (orange)
• beta=40 (yellow)
• beta=50 (lighter green)
• beta=60 (darker green)
• beta=70 (sky blue)
• beta=80 (darker blue)
• beta=90 (violet)

Plot of raw reward:

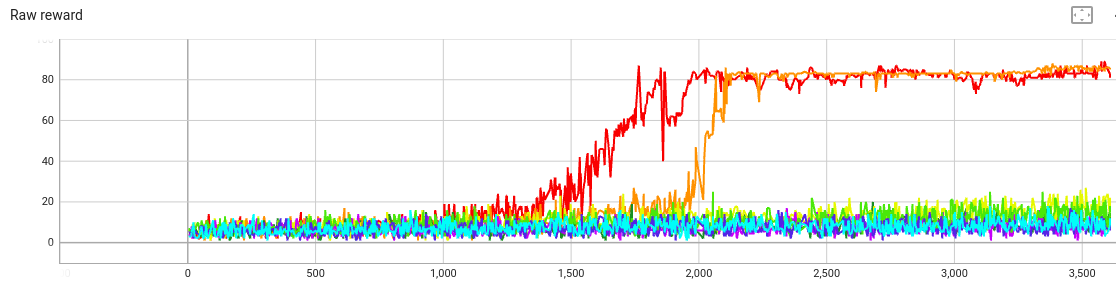
That’s a crowded graph. The key feature is that beta=20 and beta=30 both seem too weak—gradient descent is able to optimize alliteration at the expense of coherence. (The last text from the beta=20 train starts “Once upon a time there was a bird who was walking through the tall trees to get to the tall trees to the tall trees to the tall trees”, and goes on like this.)

But when beta is at least 40, the KL penalty term keeps the raw reward low. Let’s extend the beta=40 train to see how much the amount of alliteration will increase.

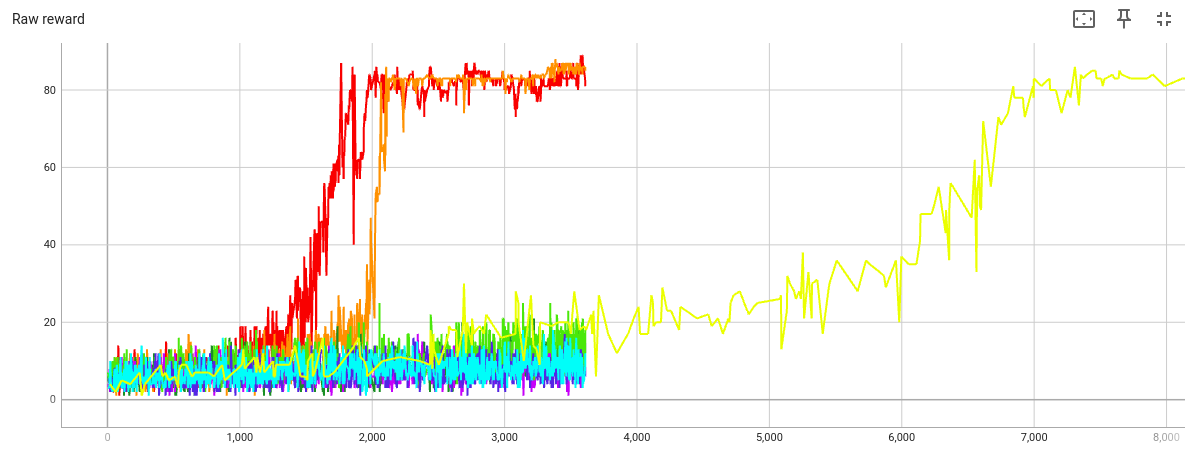
By step 7000, this train has also converged on texts with high alliteration and low variety. The first text after step 7000 is

Once upon a time there was a tall tree. The tall tree wanted to touch the tall tree. The tall tree wanted to touch the tall tree to touch the tall tree. The tall tree wanted to touch the tall tree to touch the tall tree to touch the tall tree to touch the tall tree. The tall tree wanted to touch the tall tree to touch the tall tree to touch the tall tree to touch the tall tree to touch the tall tree to touch the tall tree to touch the tall tree to

All following texts are almost identical to that one.

But the graph suggests that at step 5000, the model was still generating a variety of stories. Here are the first through fourth stories after step 5000 (the first story is the one from the introduction):

Once upon a time, there was a tall tree. The tall tree was in the middle of a park. One day, a little girl wanted to touch the tall tree. She started to walk towards the tall tree. When she got to the tall tree, she started to touch the branches. Suddenly, the tree started to grow taller and taller! The little girl was amazed and she ran away from the tall tree. She kept running and she forgot about the tall tree. She

Once upon a time, there was a little girl. She was walking in the woods when she saw a tall tree. She walked over to the tree and saw a big hole. She stepped inside the tree to take a better look and she saw something shiny! The girl carefully stepped out of the tree. When she got nearer to the top, she saw something strange. She saw an image in the tree trunk. The image was so close that she touched it! The girl was

Once upon a time, there was a little girl. She felt sad. She walked to the top of the tree but she didn’t know what to do. So she started to cry. A big, strong tree heard her cry. So the big tree tried to help. The big tree grew very tall and strong. Then the big tree used its power to make the little girl feel happy again. The little girl thanked the strong tree for her help. Since then she never stops

Once upon a time there was a tall tree. The tree was so tall that it could touch the clouds. One day, it was raining so the tall tree began to shake. All the animals in the forest were scared of the thunderous sound and the tall tree. Then something amazing happened. Some people walked to the tall tree and saw how tall it was. They decided to build a tall tower of blocks to the top of the tall tree. The tower was made of the tall

Q: I accept that this model has alliteration (“she saw something shiny”), and its stories are coherent and varied. But why does it only talk about trees?
A: My guess is that the unmodified language model (LM) is reasonably likely to generate “tall tree”. Then RLOO amplifies that trend. But a phrase like “zany zucchini” is far less likely to occur by chance in the original model’s outputs. So RLOO can’t push the weights in that direction because it never has the chance.

Moreover, I speculate that the TinyStories LM doesn’t understand what alliteration is, so it finds sentences with high reward by trial and error. But LLMs do know what alliteration is, so I speculate that enough RL would trigger an LLM’s “alliteration neuron”, and then it would start generating alliterative text that wasn’t in the RL training data so far.

Q: How would you make this model do alliteration with other letters besides s and t?
A: Probably this would require changing the reward function to give more reward if there’s alliteration with rare letters. The KL penalty alone can’t fix this, since the original LM will think that “tall tree” is more likely than “zany zucchini”, so the KL penalty wouldn’t favor the latter.